1.2 Linear and Quadratic Discriminant Analysis

1.2 线性与二次方判定分析(Linear and Quadratic Discriminant Analysis)

线性判定分析(discriminant_analysis.LinearDiscriminantAnalysis)和二次方型判定分析(discriminant_analysis.QuadraticDiscriminantAnalysis)是两种传统的分类器，和名字相对应，它们分别对应着线性和二次方型的决策表面。
这些模型的优点在于拥有易于计算的存在的结果，原生支持多分类，实践证明效果良好而且没有需要优化的超参数。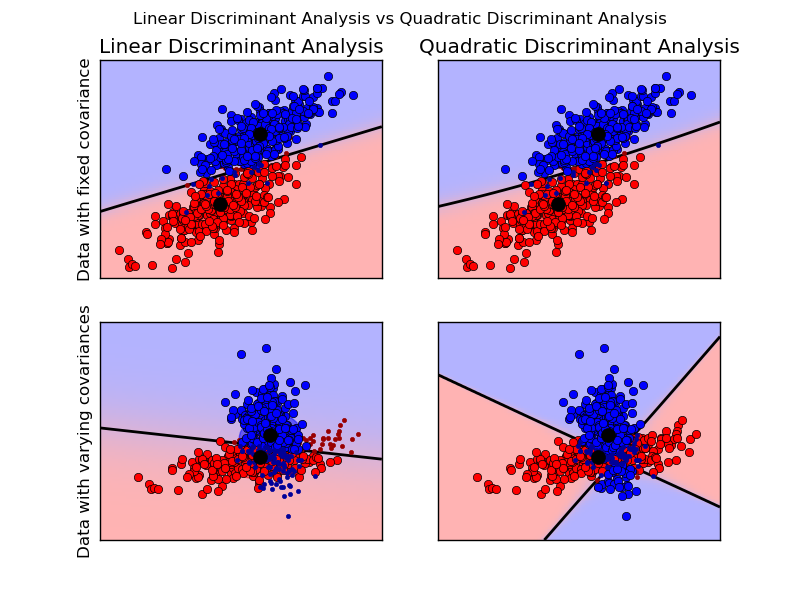


上图中显示了线性和二次型判定分析中的决策面的结果，下面一行体现了线性分析只能学习线性决策面，二次型分析则可以学习更加复杂的二次型决策面，因此也变得更加灵活。
Examples

• Linear and Quadratic Discriminant Analysis with confidence ellipsoid:Comparison of LDA and QDA on synthetic data.

1.2.1 使用线性分析进行降维(Dimensionality reduction using Linear Discriminant Analysis)

discriminant_analysis.LinearDiscriminantAnalysis可以被用于监督式降维，通过将输入数据投影到一个线性子空间中，这个子空间中由能够最大化分离类别的方向的向量作为基向量。这是一种很有效的降维方式，特别是在多类别任务中。
实现如discriminant_analysis.LinearDiscriminantAnalysis.transform,降维后的维度可以使用参数n_components设置，但这个参数不会影响discriminant_analysis.LinearDiscriminantAnalysis.fit和discriminant_analysis.LinearDiscriminantAnalysis.predict
Examples
Comparison of LDA and PCA 2D projection of Iris dataset: Comparison of LDA and PCA for dimensionality reduction of the Iris dataset

1.2.2. LDA 和QDA的数学公式(Mathematical formulation of the LDA and QDA classifiers)

LDA和QDA都可以通过对数据的条件分布进行建模的简单模型推导出来，每一类别的条件分布可以表示为

$$P(X|y=k)$$

那么预测结果可以用贝叶斯公式得出：

$$P(y=k|X) = \frac{P(X|y=k)P(y=k)}{P(X)}=\frac{P(X|y=k)P(y=k)}{ \sum_l P(X|y=l)P(y=l)}$$

然后我们选择使得预测概率最大的k作为分类结果。